About a month ago, this paper was published and immediately made waves. It builds on another paper, The Platonic Representation Hypothesis, which also stirred significant interest when it came out, and claims to reinforce it substantially, surprisingly so. Along the way, it also demonstrates how to leverage this intriguing theoretical achievement into a significant breakthrough in information extraction. The magnitude of the buzz was the result of all of these elements, combined with writing that encourages an overly bombastic reading of what the paper actually shows. Let’s clarify things a bit.
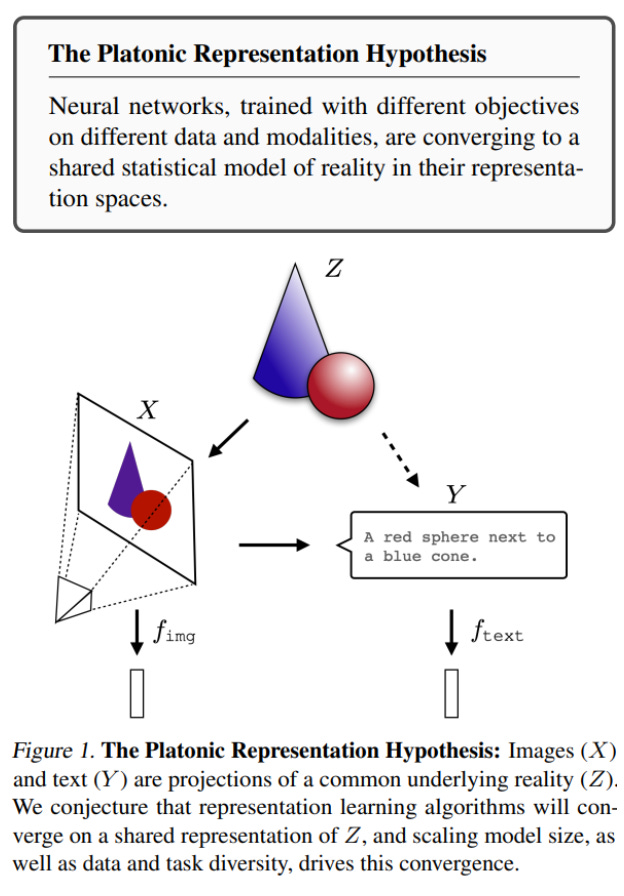
Data, whether textual, visual, or other ultimately comes from that process we call reality. As large models are trained on more data, more varied, across many diverse tasks and their representations increasingly tend to converge toward the shared reality underlying it all, the "true" latent space that enables optimal inference. That was the claim advanced by the original paper and it attempted to demonstrate this via various metrics and comparisons. So far, so good.
The new paper sets out to make a seemingly stronger and more “constructive” claim:
It argues that this universal latent space for text representations can actually be learned, and that it can be used to "translate" from one representation space to another without any aligned data (i.e., without having access to both encodings of the same input), and in fact without access to one of the models at all, just to some of its embedding samples.
Then, given the ability to translate from the space of an unknown model to one we control, it becomes possible to reveal properties about the information encoded in the unknown model and even to reconstruct it using known "embedding inversion" techniques.
So how does it all work? First, let’s sharpen two points where the paper is guilty of "over-promising" (which will hopefully soften when it hits the wall of peer review):
The original paper spoke of a single, shared space that unifies all models namely the reality behind the manifold of reflections. This was the theoretical heart of the matter, justifying a philosophical reference that goes back 2400 years. The current paper, however, does not achieve such a unified representation. Its learned representation bridges only between a specific pair of models at a time. This is definitely a step in the right direction but it’s not quite there yet.
The original paper dealt with alignment between different modalities (and more), such as matching object names (in text models) to their images (in vision models) - see image. That’s a far deeper and more significant challenge than aligning just between two text models which is what the new paper focuses on. (It does touch on CLIP, but that’s essentially a text model whose construction already aligns it with image data; there’s not much to learn from that in our context)
Now that we’ve toned down the hype a bit, let’s dive into the actual content because it's still quite interesting. As we said, the paper builds mappings from embedding space X to embedding space Y. It does this using five trained mappings, implemented as neural networks:
Mappings A1 and A2 map from X and Y to a shared embedding space Z, respectively.
Mapping T aligns the embeddings after A1 and A2 into a shared latent space Z.
Mappings B1 and B2 map the embeddings from Z back to X and Y, respectively.
On top of these, the following can be defined:
"Translation" mappings: F1 = B2∘T∘A1, F2=B1∘T∘A2. These are mapping from one original embedding space (X to Y, and Y to X) to another.
"Self-mappings": R1=B1∘T∘A1R1, R2=B2∘T∘A2. These ones map X (or Y) to itself via the shared embedding space using T.
Now that we’ve defined this long chain of mappings, let’s explain the structure of the full loss function. It’s composed of several parts:
The first loss enforces that the distribution of the mappings from X, after being passed through F1 to Y, should resemble the native distribution of Y. This is done using GANs (Generative Adversarial Networks), which previously dominated image generation before diffusion models. GANs train two models with opposing losses: the generator model (F1) is trained to make the mapped Xs look like Ys, while the discriminator model (D1) is trained to distinguish between real Ys and F1 outputs. If training converges, you get a strong generator (F1) that "fools" a strong discriminator (D1). The same setup is used for F2 and D2. The paper uses the classic GAN formulation from Goodfellow's 2014 paper.
Additionally, two more GANs are trained for the latent representations coming from both X and Y i.e., the generative model here is T∘A1, trained as above. Another GAN is trained for T∘A2. These four losses make up the first part of the total loss.
The second part of the loss is a reconstruction loss, ensuring that any embedding passed from X (or Y) to the shared space can be accurately mapped back to itself via B1 (or B2).
The third part is a cycle-consistency loss, ensuring that a representation passed from X to Y (via F1), and then back to X (via F2), ends up close to the original input and likewise in the other direction.
The final part of the loss ensures that pairwise distances between different embeddings from X (or Y) are preserved during translation to Y (or X).
In the end, the total loss includes all these components. This is how the shared representation is learned without any aligned data at all! Impressively, the learned mapping even generalizes to very different text distributions, making this bridging technique quite general. But for those details as well as for the intriguing application of this technique to information extraction, you’ll have to turn to the paper itself :)