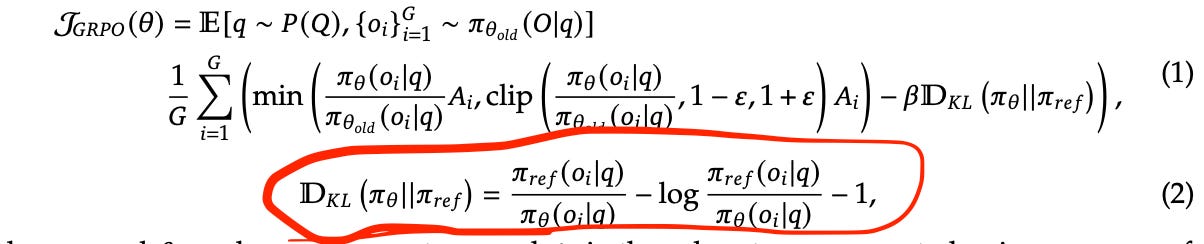An unusual look of the KL-Divergence Term in Deep Seek R1 Training Objective?

DeepSeek Blog Series: based on http://joschu.net/blog/kl-approx.html

I’d like to express my gratitude to Gal Hyams for directing me to Joe Schulman’s insightful blog.

Introduction:

I am continuing my investigation into the ideas presented in the Deep Seek R1 paper paper, focusing now on the GRPO optimization objective. This objective consists of two key components: a reward maximization term (similar to PPO) and a Kullback-Leibler (KL) divergence regularization term. The KL term serves to ensure that the LLM’s policy (i.e., the token distribution conditioned on the context) remains close to the initial reference policy.

But this term looks a bits strange - it doesn’t look like KL divergence. This blog explains why how Formula 2 is related to KL.

KL Divergence with Monte Carlo: The Short Explanation

KL divergence measures the difference between two probability distributions q(x) and p(x). Direct computation is often infeasible due to high computational costs or intractable sums, necessitating efficient approximation methods. In this case we usually use Monte-Carlo methods for estimating such quantities. And this formula is actually a low-variance and almost unbiased Monte-Carlo based estimator of KL-divergence between π_θ and π_ref when π_θ and π_ref are close.

KL Divergence and Its Approximation

The KL divergence is formally defined as:

\(KL(q||p) = \sum_x q(x) \log \frac{q(x)}{p(x)} = \mathbb{E}_{x \sim q} \left[ \log \frac{q(x)}{p(x)} \right] \)

• q(x): Distribution to sample from (known as the proposal distribution). It is π_θ in Formula (2).

• p(x): Target distribution being compared to. π_ref in Formula (2).

Challenges:

1. No closed-form solution for many distributions.

2. High computational cost of summing over x in high-dimensional or continuous spaces like we have in the RLHF training objective.

2. Monte Carlo Estimators of KL-divergence

The KL divergence is approximated by sampling x∼q(x) and constructing estimators. Let’s analyze here 3 possible estimators for KL between p(x) and q(x):

• Naive (k1​)

• Squared-log (k2​)

• Control-variate-based Bregman estimator (k3​).

a) Naïve Estimator (k1​):

The most straightforward Monte Carlo estimator of KL divergence is (remember that we sample with q(x):

\(k_1 = \log \frac{q(x)}{p_(x)} = -\log r, \quad r = \frac{p(x)}{q(x)} \)

Properties:

• Unbiased (expected value equals the true KL divergence).

• High variance because log⁡(r) can be negative or large.

• KL divergence is always positive, but k1 can yield highly fluctuating negative values.

b) Squared Log Estimator (k2​):

\(k_2 = \frac{1}{2} (\log r)^2\)

Properties:

• Biased, but with much lower variance than k1 (its mean doesn’t equal to the KL divergence between p(x) and q(x)​.

• Intuitively better because it measures the magnitude of log⁡(r) without introducing sign flips.

Connection to f-divergences:

F-divergence is a broader class of functions measuring difference between probability distributions. KL divergence is a particular case of f-divergence. F-divergences are defined as:

\(D_f(p||q) = \mathbb{E}_{x \sim q} [f(r)], \quad r = \frac{p(x)}{q(x)}\)

For KL divergence, f(r)=−log⁡(r) whereas for k2 we have:

\(f(r)= \frac{1}{2} (\log r)^2 = \frac{1}{2} \large[\log\large( \frac{p(x)}{q(x)}\large)\large]^2\)

An interesting mathematical fact about f(r) that t approximates KL divergence between to second order when q≈p. Namely if p and q are similar distribution f(r) is constitutes an adequate estimator for KL(p||q).

---

c) Bregman Estimator (k3):

The third estimator is:

\(k_3 = (r - 1) - \log r = \frac{p(x)}{q(x)}\ - \log\large(\frac{p(x)}{q(x)}\large) - 1\)

Properties:

• Unbiased: Always matches the true KL divergence in expectation. It can be quite easily proved.

• Derived using a control variate approach: k1 is adjusted by adding a term with zero expectation but negatively correlated with k1​, reducing variance (we want low-variance estimators, remember?).

• Always positive: Utilizes convexity of log⁡(x) to ensure positivity.

Estimator Comparison:

• k1​: Unbiased but impractical due to high variance.

• k2​: Low variance but introduces small bias, especially for larger divergences.

• k3k​: The best of both worlds, offering low variance and unbiased estimation.

k3​ stands out as the most effective estimator for KL divergence, especially in applications that demand both accuracy and computational efficiency. Its basis in Bregman divergence theory guarantees that it is positive, unbiased, and stable.

Upon closely examining Formula 2 in the paper, you’ll notice k3 explicitly. It seems we’ve successfully uncovered its origins and understood the reasoning behind it.